We want to write a function that takes a non-empty array of distinct integers and an integer representing a target sum. If any two numbers in the input array sum up to the target sum, the function should return them in an array, in any order. If no two numbers sum up to the target sum, the process should return an empty array.
Intended Audience
This article teaches you how to approach and solve the two summation challenge. Therefore, you should be familiar with some basic understanding of programming constructs. And also, we’d be covering the time and space complexity of this algorithm.
First Approach
My first approach would be to go through the array of integers in a brute force manner. Suppose we have an array of numbers [ 1, 2, 3 ]. We need to figure out all the two-element combinations it can have. If we think about it, we would probably end up doing something like this:
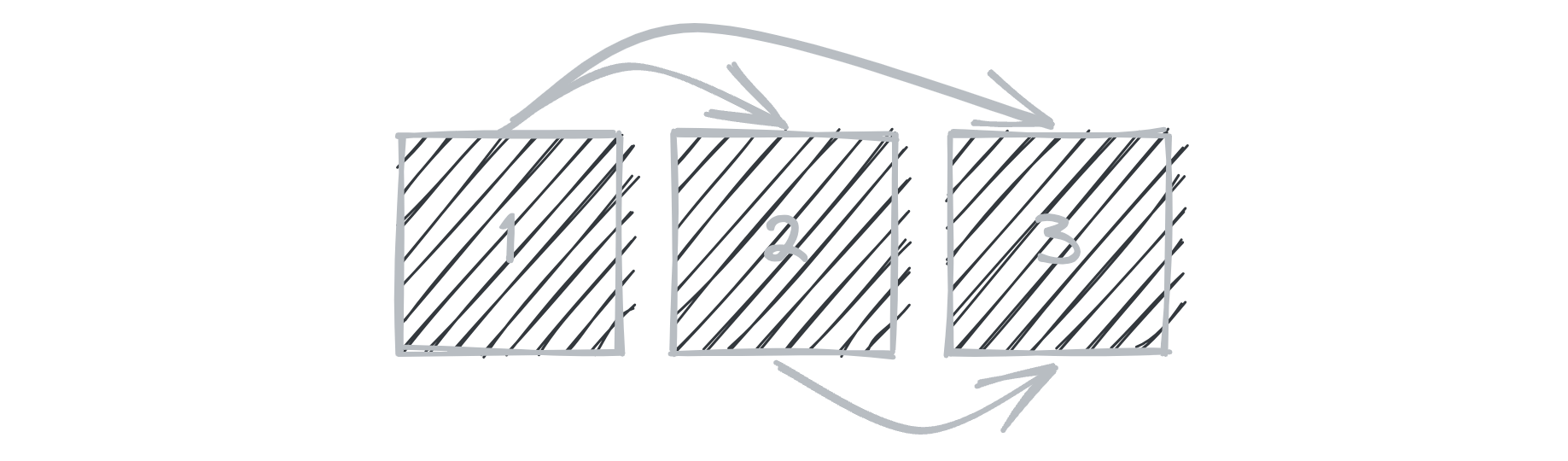
Conceptually in this approach, we try to achieve a reducing set of combinations for two numbers and do some calculation with it. If we can align this approach as a solution to our challenge statement, we can write a brute force algorithm like the following:
- An outer loop which goes through each of element until
- An inner loop which goes through
- A condition to check the summation
Program Input — Say we have an array
[ -1, 5, -4, 8, 7, 1, 3, 11 ]and a target sum14. Now let’s transform above steps into a pseudocode.
function solve(array, targetSum) {
for (let x = 0; x < array.length - 1; x++) {
for (let y = x + 1; y < array.length; y++) {
if (array[x] + array[y] === targetSum) {
return [array[x], array[y]];
}
}
}
return [];
}
solve([-1, 5, -4, 8, 7, 1, 3, 11], 14) // [3, 11]If we were to execute this algorithm, what are the different combinations we go through? Let’s write down the iterations and their respective combinations manually.
| Iteration | Checked Combinations |
|---|---|
| 1 | (-1,5), (-1,-4), (-1,8), (-1,7), (-1,1), (-1,3), (-1,11) |
| 2 | (5,-4), (5,8), (5,7), (5,1), (5,3), (5,11) |
| 3 | (-4,8), (-4,7), (-4,1), (-4,3), (-4,11) |
| 4 | (8,7), (8,1), (8,3), (8,11) |
| 5 | (7,1), (7,3), (7,11) |
| 6 | (1,3), (1,11) |
| 7 | (3,11) |
Did you see that? In worst-case scenario we had to evaluate pairs and in the th iteration we found our matching number pair . However, it’s not the same always. It will change based on the indices and therefore combinations will be lesser if we break out of the loop after a successful match.
Combinations
In mathematics, combinations are the number of possible arrangements in a collection of items where the order of the selection does not matter.
What we just did is very much similar to enumerative combinatorics. You can see that our approach is awfully inefficient in doing that. There are techniques that one could use to optimize combination problems. But simply for our first approach, it is not needed at all. Instead, I’m leaving this here because this is just one way we could think of the problem.
If you are interested in learning combinatorics, you can refer to Sal’s explanation on Khan Academy. If you’re super serious about it, I’d recommend you read Concrete Mathematics and Enumerative Combinatorics books to solidify your knowledge in it.
Now let’s do a quick analysis of our first solution.
Problem Analysis
While this works pretty well for smaller arrays, it won’t scale nicely for larger arrays. The algorithm we just wrote is pretty slow.
Time Complexity — So, to reiterate, we have an outer loop that goes through the and an inner loop that goes until to check the combination of two numbers. This means that we would need to iterate over .
In worst-case scenario, we do 1 iterations just to check whether we have a matching pair.
This algorithm has a polynomial time complexity where it grows proportionally to the square of the input size . Unfortunately our algorithm takes time to complete.
Space Complexity — We only use two for loops which involves constant variables as indexes and . And also, we don’t use any extra space. So, our algorithm’s space complexity will always be .
We know that first approach is bad but can we improve the algorithm and make it a bit faster? What happens if we first sort the array?
Second Approach
There’s a second way of solving this problem. And it’s slightly better than the first one. Initially, in the challenge statement, I didn’t mention whether the array is sorted or not. So, what if we sort the array first in ascending order and then figure out a way to solve this?
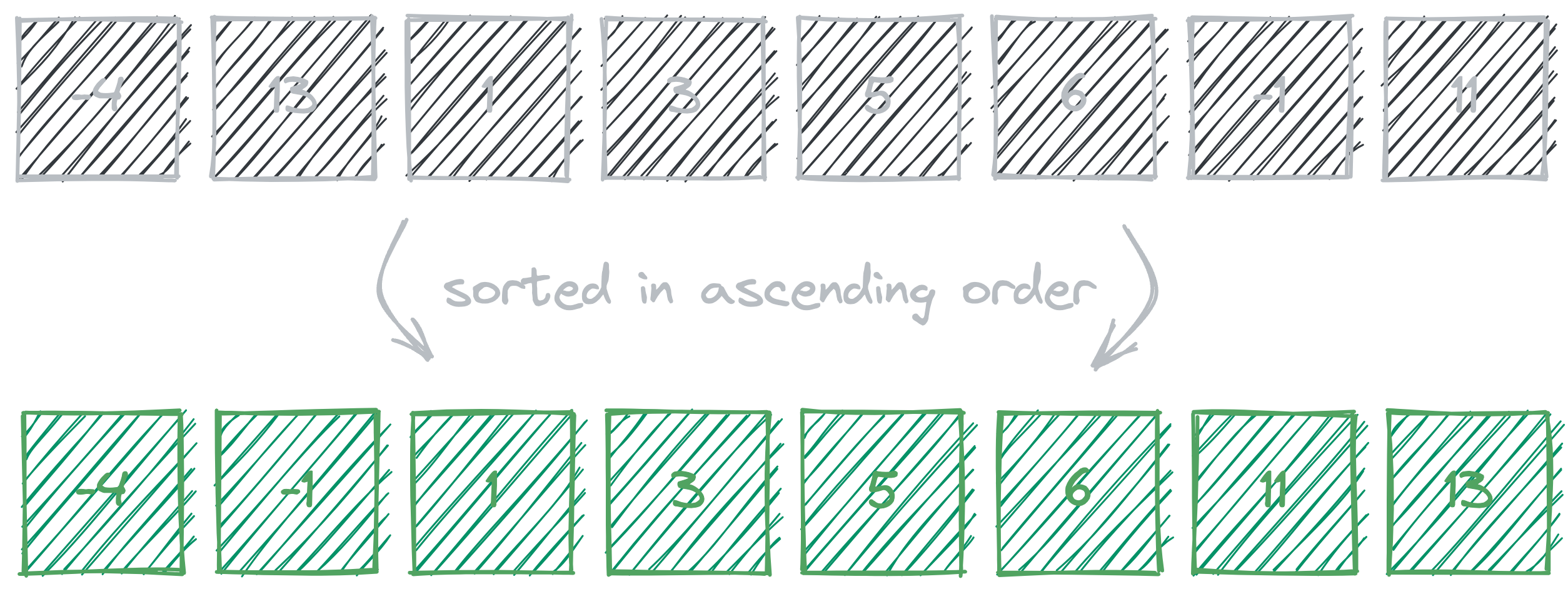
Program Input — Say we are given a new array
[ -4, 13, 1, 3, 5, 6, -1, 11 ]and a target sum of10. Let’s use these inputs for our second approach.
First Operation
First, we have to sort the array in ascending order2. In order for the algorithm to work this must be done and then only we can continue.
Second Operation
Then we can allocate two pointers from left and right to walk through the elements times and operate on these two numbers.

This way we can solve the problem more optimally instead of using two for loops. With a reasonable sorting algorithm like mergesort or quicksort we could sort the array in time. But remember we still have to walk through our times which is equivalent to .
Third Operation (doing the summation)
So far, now we know the array must be sorted first, and we need two pointers to compare. The core logic of this approach is to drive algorithm’s state using three predicates. We need to check whether the sum of :
- Is it equal to target sum?
- Is it less than target sum?
- Is it greater than target sum?
Let’s try to write down the algorithm. Remember that, up to this point, we assume that we have already sorted the array and allocated the two pointers. Now it is time to evaluate the above conditions against each pair in every th iteration.
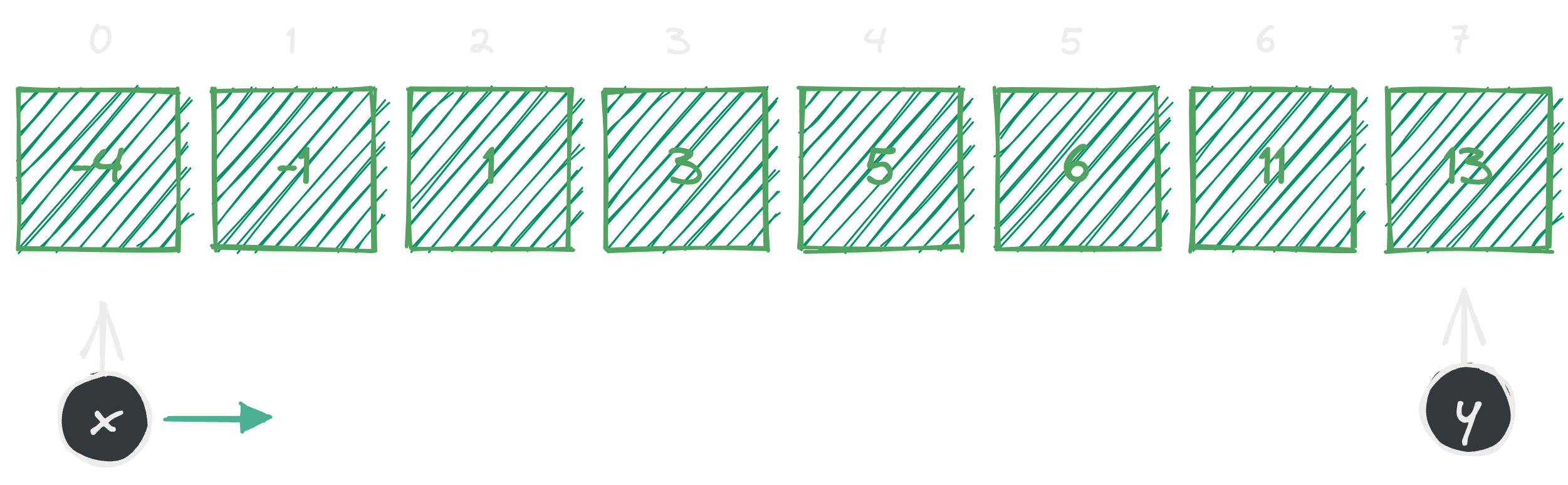
Our loop starts from and . At this point our ‘s element is and ‘s element is (see figure 4). If we add up those two numbers together, we get a total of which is less than our target sum . In this case we move the pointer to the right side. Basically, incrementing ‘s index by . That way we can guarantee that in next iteration we would always get a sum .
Alright, in the last iteration we moved by and now we are at and (see figure 5). Once again, if we sum up and we get a total of . Now, this is larger than our expected target sum. In this case we move the pointer to left side. Saying that we want to decrement our pointer by .

Got the point? We do this iteratively until matching the target sum or until and meets together at the same index.
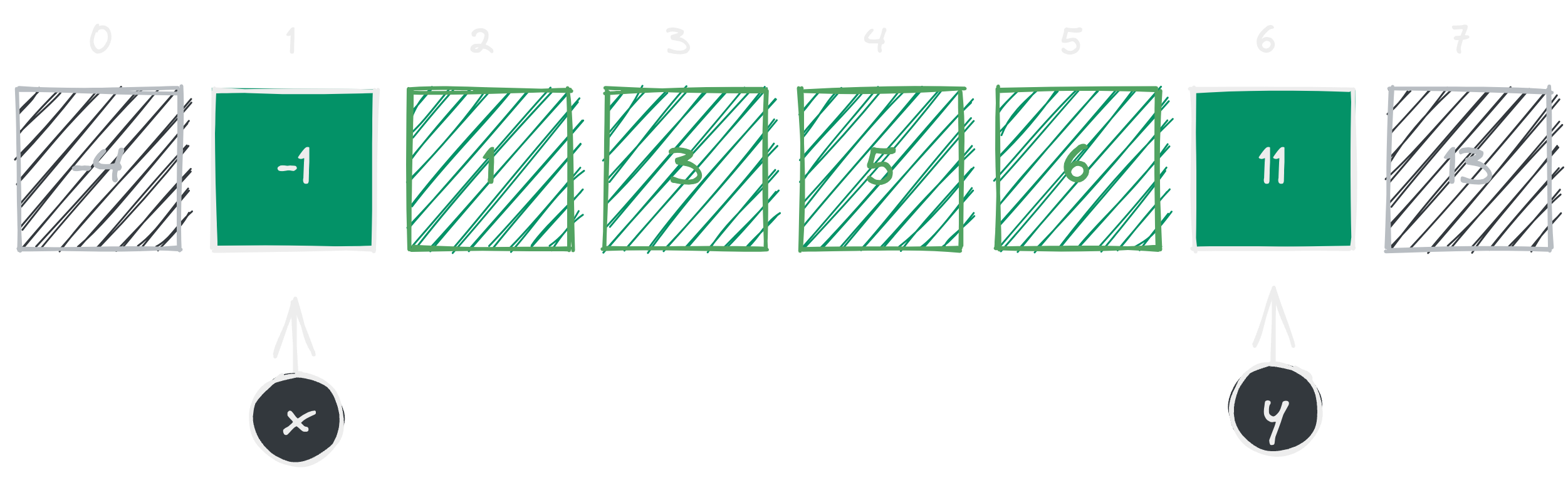
Well, would you look at that? We reduced the number of iterations we have to go through! We have accomplished significant progress in making this algorithm a bit faster. Now that we found our number pair, we can finally return the result and halt the algorithm. Let’s write the JavaScript code for this algorithm now.
function solve(array, targetSum) {
const sorted = array.sort((a, b) => a - b);
let x = 0;
let y = sorted.length - 1;
while (x < y) {
if (sorted[x] + sorted[y] === targetSum) {
return [sorted[x], sorted[y]];
} else if (sorted[x] + sorted[y] < targetSum) {
x++;
} else {
y--;
}
}
return [];
}While this approach is slightly better than the first, we are back to square one. Why? Well, it’s the same reason as before; it does not scale well enough for larger arrays. Let me show you the problem.
Problem Analysis
First, we need to understand the cost of sorting things. Browsers have implemented stable and well optimized algorithms for Array.sort(). But assume that the sort function chose mergesort as our sorting algorithm.
It is guaranteed that mergesort runs in time using space. And since we only used one while loop to drive the state of and pointers, we get which is equivalent to in total time3 and for space.
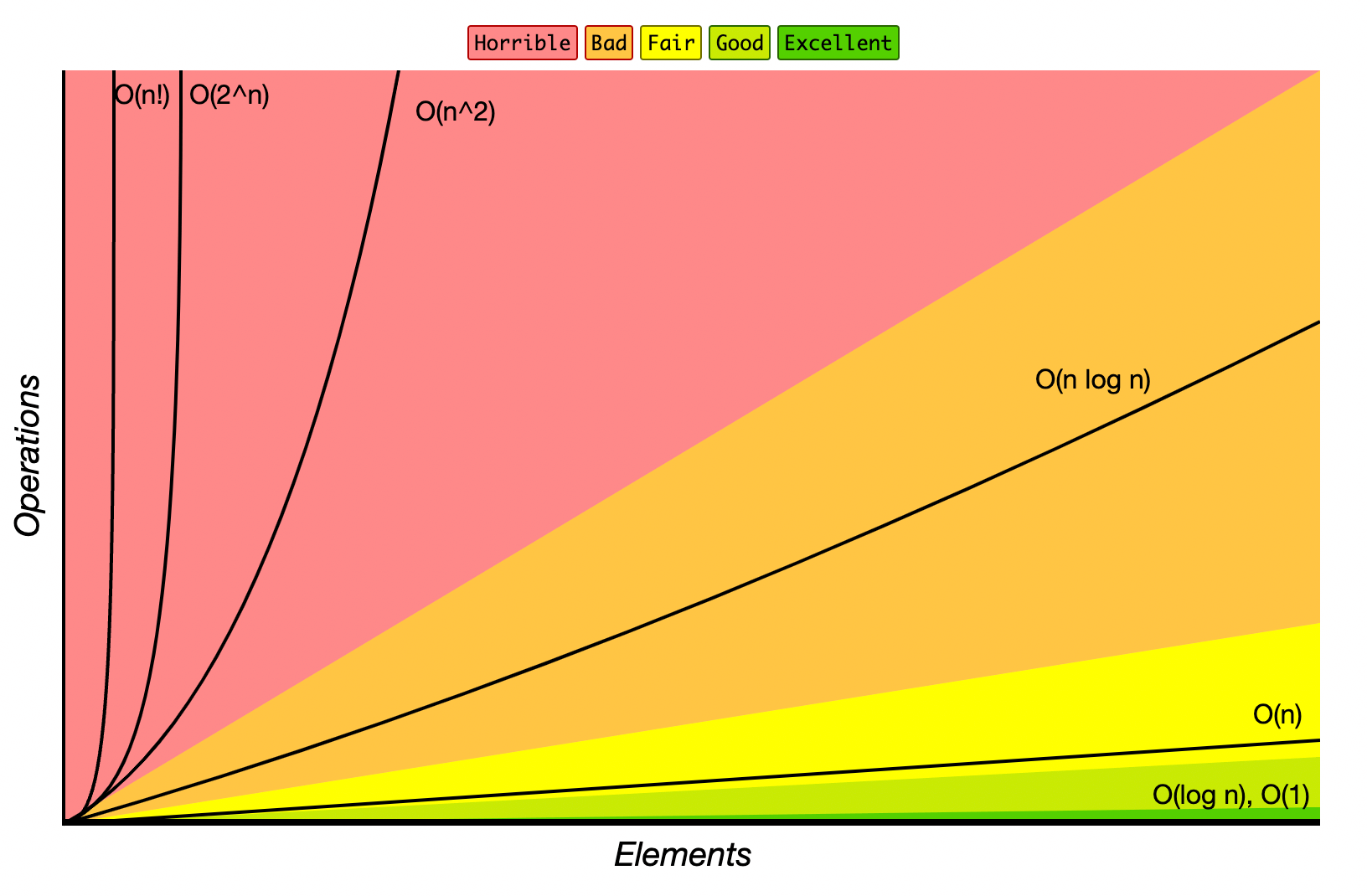
The algorithm we wrote runs in linearithmic time which tells us its complexity grows proportionally to the array input size with a logarithmic factor. What can we do about it? Can we solve it in linear time?
Dynamic Approach
Up until now, all the approaches we have taken is not very optimal from a time standpoint. Fortunately, there’s one other way of solving this problem in a much cooler way. You might have thought about this already from the previous approach. But first, let’s list down the things we already know:
- We know what our target sum is (let it be ).
- We already know one of our addends4 (let it be ).
So, basically we have two variables at hand before even doing any operations. So, we could write an equation like to represent it (where is unknown). Where we can isolate the unknown variable. Say for example,
Inverse Operations
To isolate a variable, we cancel out (or undo) operations on the same side of the equation as the variable of interest while maintaining the equality of the equation.
This can be done by performing inverse operations on the terms that need to be removed so that the variable of interest is isolated. Subtraction cancels out addition, and vice versa, and multiplication cancels out division, and vice versa.
Now we can find the unknown variable without any combinations or two pointers. The only caveat is that we need a way to memorize this calculated value as we go through the array.
Solution
Using some extra space is okay as long as its complexity grows in a reasonable size. Now what do you think? For our solution should we use a hashmap? What about a set?
You’d see a lot of examples of two summation problem’s dynamic approach in the internet uses a hashmap auxiliary space implementation. But we really do not need key-value pairs for our solution. Instead, simply we can use a set of numbers to track the inversion results.
Formal Proof
There exists such that may or may not be a member of .
Elaboration
We need a loop that goes through each element of the array starting from index . We need to calculate the inverse set within the loop5 so, we create an empty set and then for each element we calculate 6 and now we can place a predicate that checks existence in inverse set like then return if is true. Otherwise, we union our inverse set with the calculated value where and we keep on looping until .
Switching to New Inputs — For this approach let’s use the array
[ -7, -5, -3, -1, 0, 1, 3, 5, 7 ]and the target sum-5.
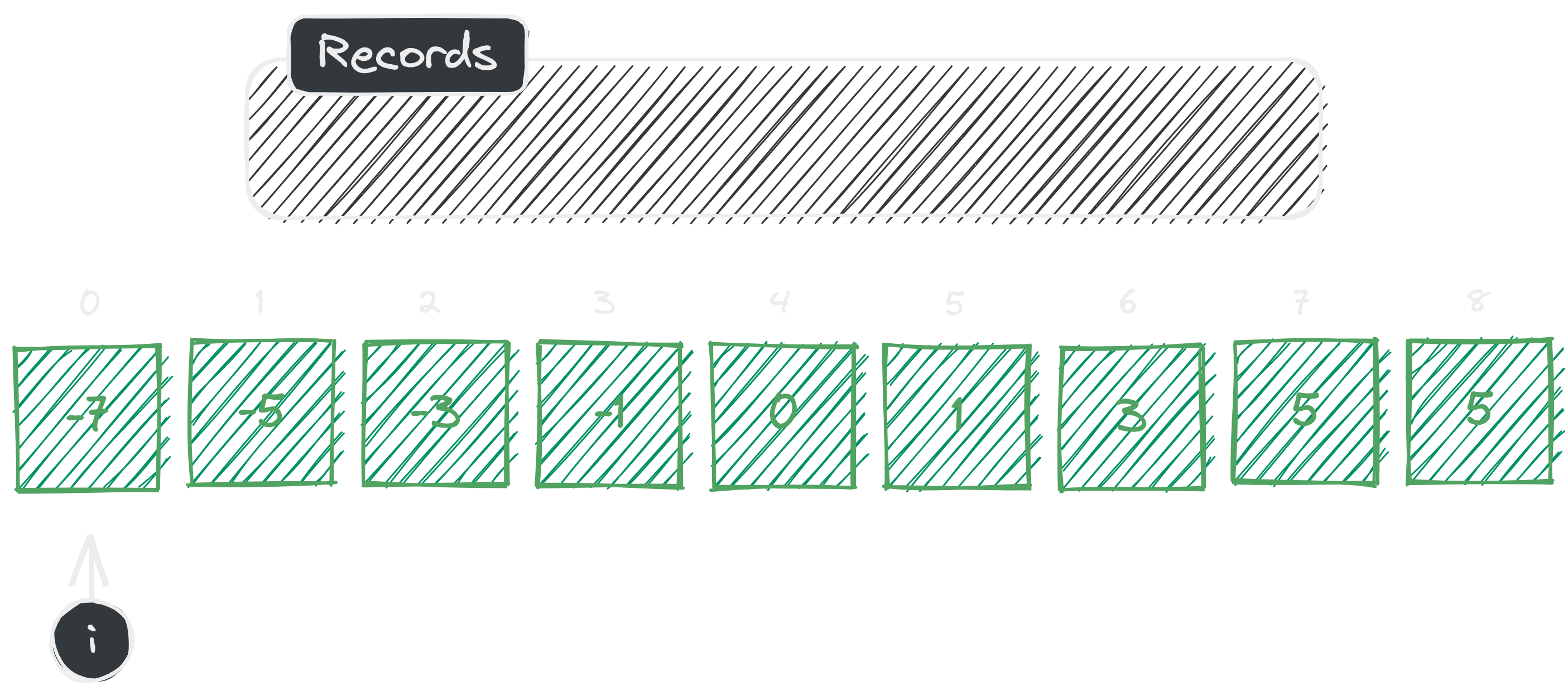
As illustrated, in the first iteration we start off with an empty set named . Initially our loop starts from index where is the index variable. In the first iteration we don’t have any elements. So, therefore we immediately add the calculated value to the set and move on to the next element.
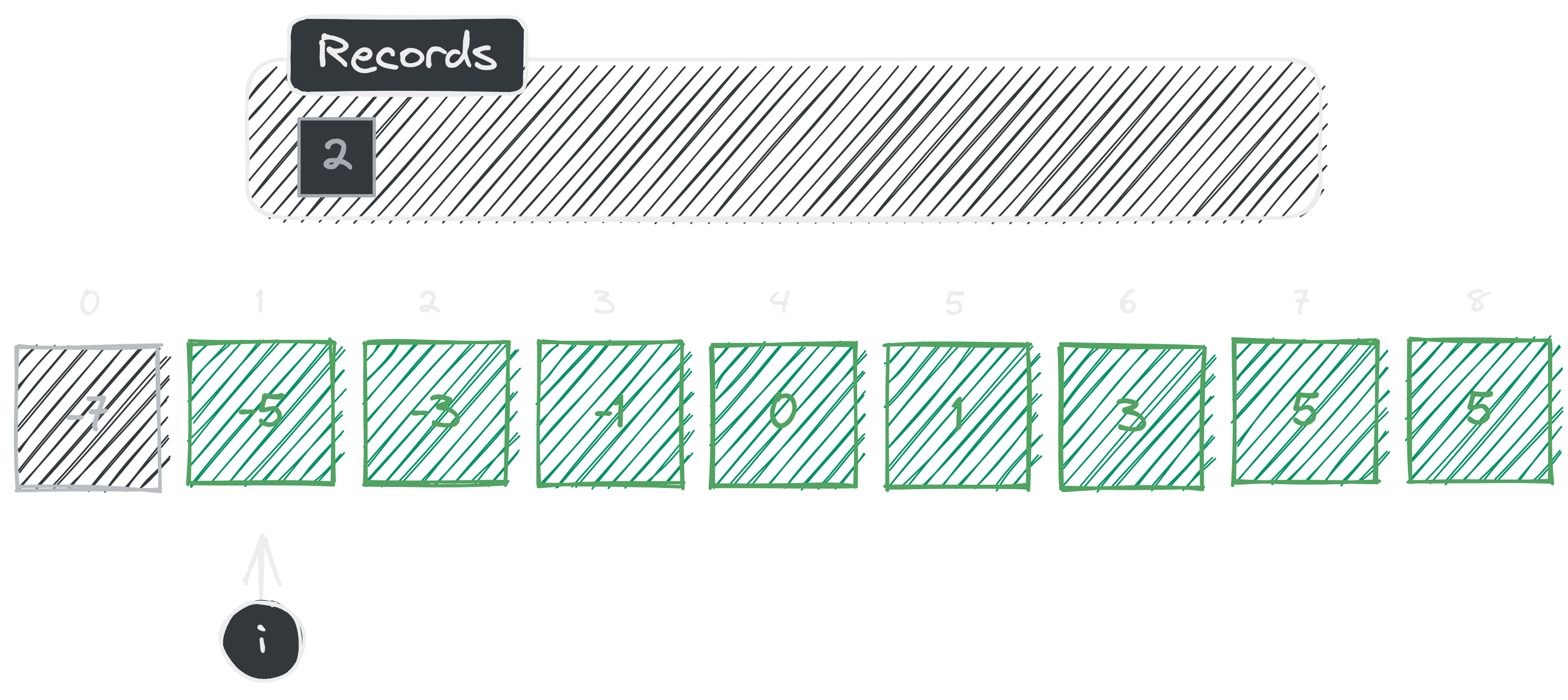
In the second iteration, first we check whether element at index is an element of . We can see that so, we add our inverse calculation to set and continue.
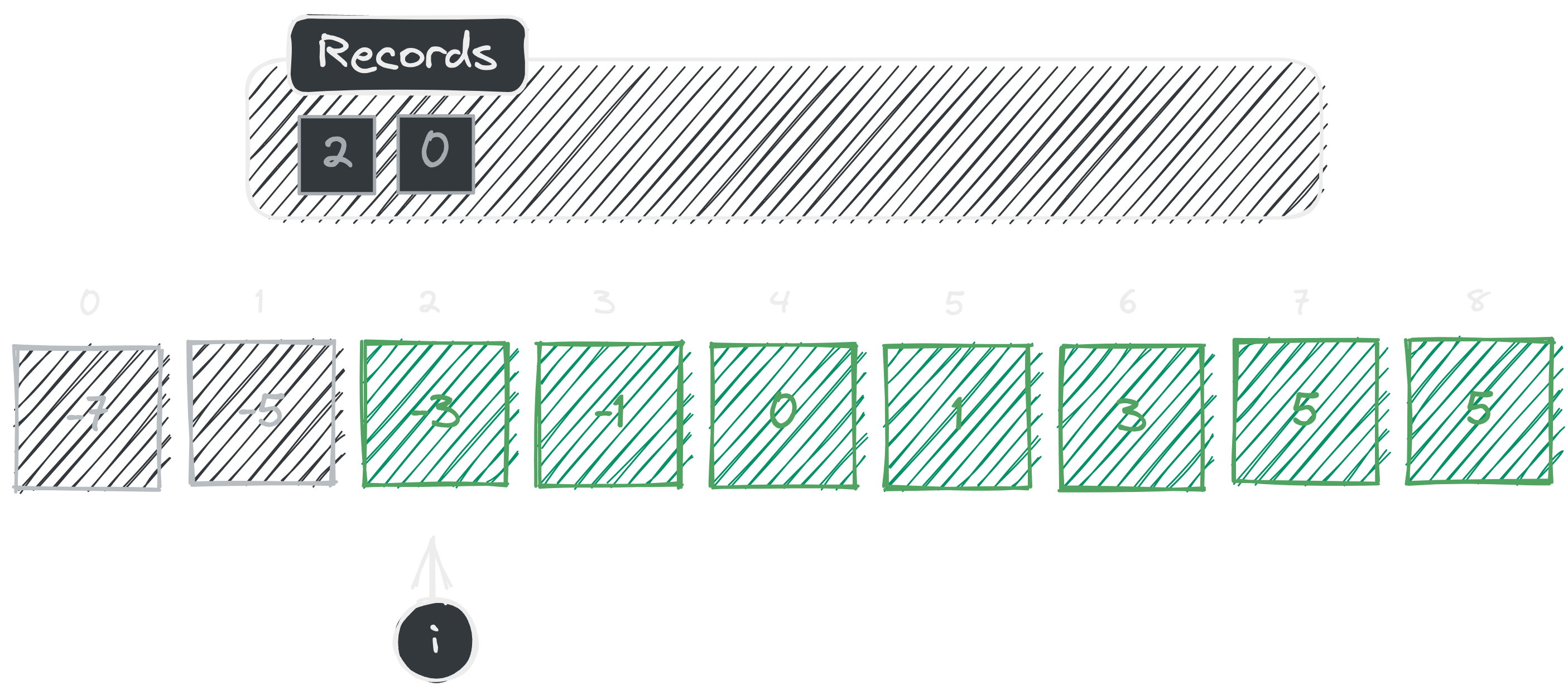
In the third iteration, again we check whether element at index is an element of . We can see that so, we do our inverse calculation and add it to set and continue.
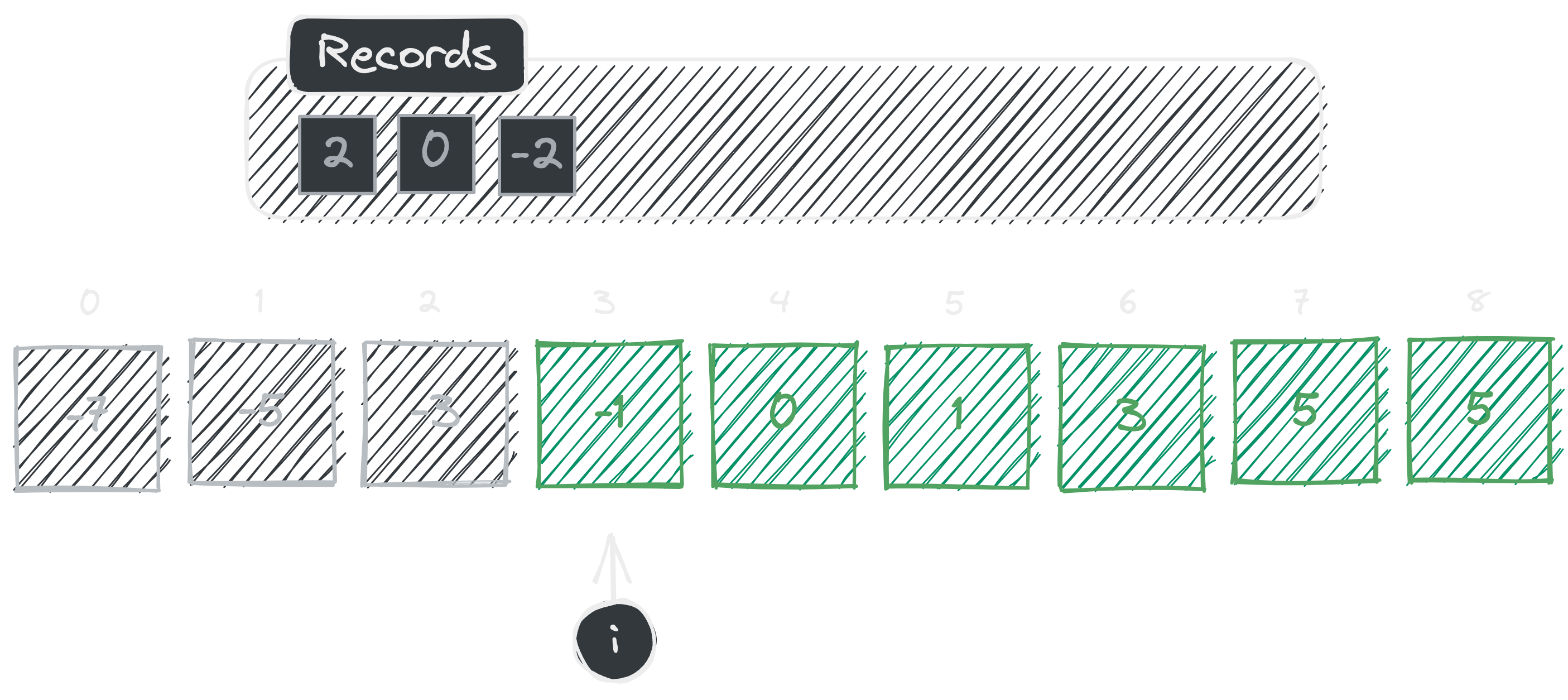
Fourth iteration already! Again we check whether element at index is an element of . We can see that so, we do our inverse calculation and add it to set and continue.
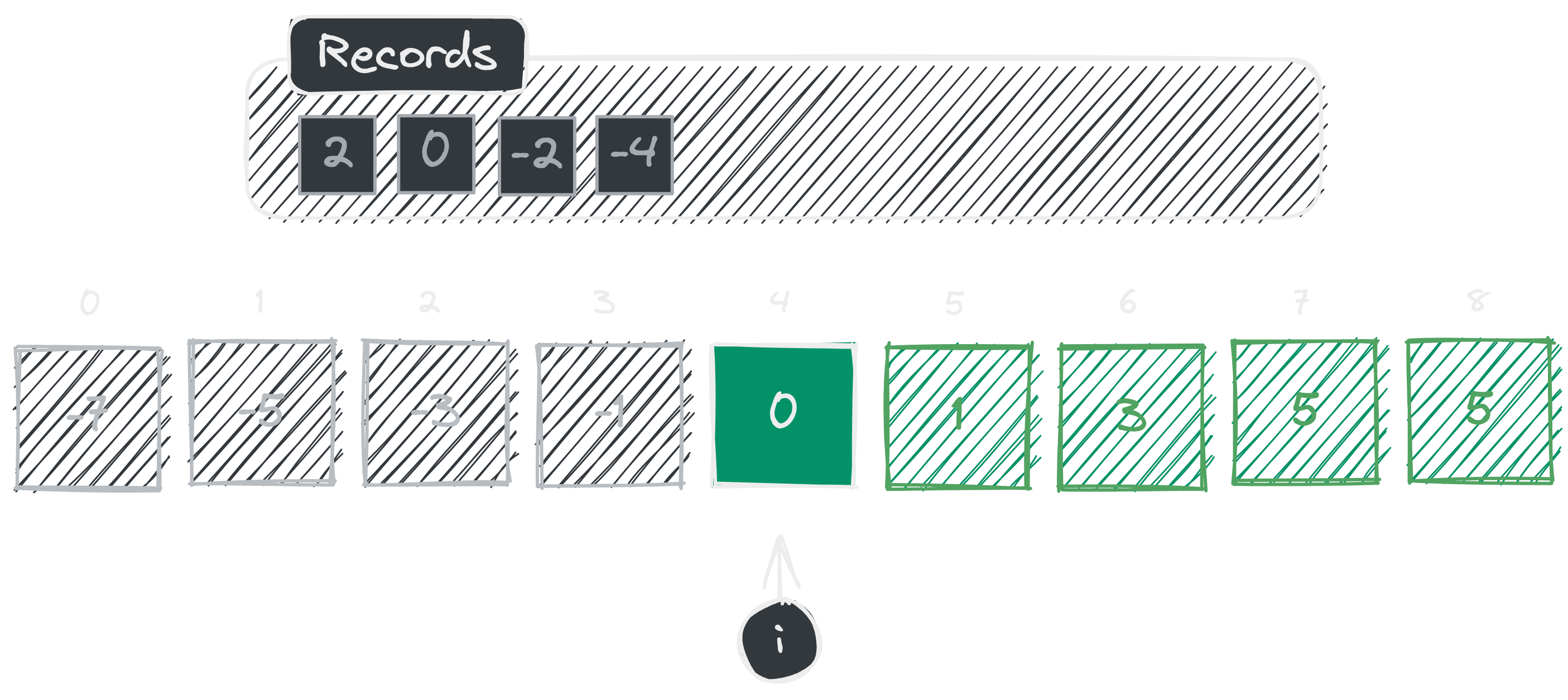
We are in the fifth iteration! And would you look at that! We just found in our set . This means our inverse got a match! Now we can return these two elements like where is .
Woohoo now we have an idea on how it works, let’s write the pseudocode.
function solve(array, targetSum) {
const records = new Set();
for (let x = 0; x < array.length; x++) {
let y = targetSum - array[x];
if (records.has(array[x])) {
return [array[x], y];
}
records.add(y);
}
return [];
}Time & Space Complexity
In this approach we solely rely on dynamic programming techniques. And we were able to solve it in time and space complexity. This is the optimal way of solving this problem.
Summary
Overall, I think even though two summation is a very easy challenge, we can learn a lot from it. How simple algebraic equations can help to solve complex problems more elegantly.
Until next time. Thanks for reading!
Footnotes
-
Binomial derived from the combinations formula — we can say that is the number of elements we have to check, and we have to choose of them without any order to check the summation. ↩
-
You can do it either way. We can sort in descending or in ascending order. But we have to make sure we swap the comparing indexes along with the conditions. But for now let’s stick to ascending order to make things simpler. ↩
-
Remember, in time and space complexity analysis we always pick the dominant term. ↩
-
What I’m referring to is the current element while walking through the array. ↩
-
We could also do a pre-computation of the inverse set before the loop. Since it does not affect the running time of the algorithm, it’s up to you to decide! ↩